Symbolic and numerical computation together to simulate complex dynamic systems

When we think of a computer, we picture it dealing with numbers: additions, multiplications, data turning into results. This is numerical computation, the type we use every day with calculators, spreadsheets, and simulation software.
But scientific computing also has another dimension: symbolic computation. Here the computer does not process numbers, but manipulates equations and formulas, just as we would do on paper. Programs that allow this are called Computer Algebra Systems (CAS): software capable of simplifying formulas, solving systems of equations, and operating on complex mathematical models.

Symbolic computation, however, has a limitation: when equations become too complex, expressions grow exponentially—a phenomenon known as expression swell. Numerical computation, on the other hand, is fast and efficient but can become unstable if the model is ill-conditioned. The best solution? Combine both worlds.

The idea is simple but powerful:

• symbolic computation prepares the equations, simplifies them, and identifies system constraints;
• numerical computation then runs the simulation, evaluating the equations efficiently and accurately.

Depending on the problem, symbolic computation may be used only in the initial phase or interact continuously with numerical methods. The result is always the same: more robust, faster, and more reliable simulations.

An application: Differential–Algebraic Equations (DAEs)

One field in which this combined approach is particularly effective is that of Differential–Algebraic Equations (DAEs), which mix two types of relationships:

• differential, describing time evolution;
• algebraic, imposing constraints on system behavior.

DAEs are fundamental in engineering for modeling complex systems: vehicles, robots, electrical circuits, and even space missions.
They contain intrinsic constraints (such as robot joints or Kirchhoff’s laws in a circuit) that make the model realistic but also difficult to simulate.

Here symbolic computation reveals its full potential: by rewriting and simplifying DAEs, it enables numerical methods to work with greater stability and speed.

An example: a vehicle suspension system

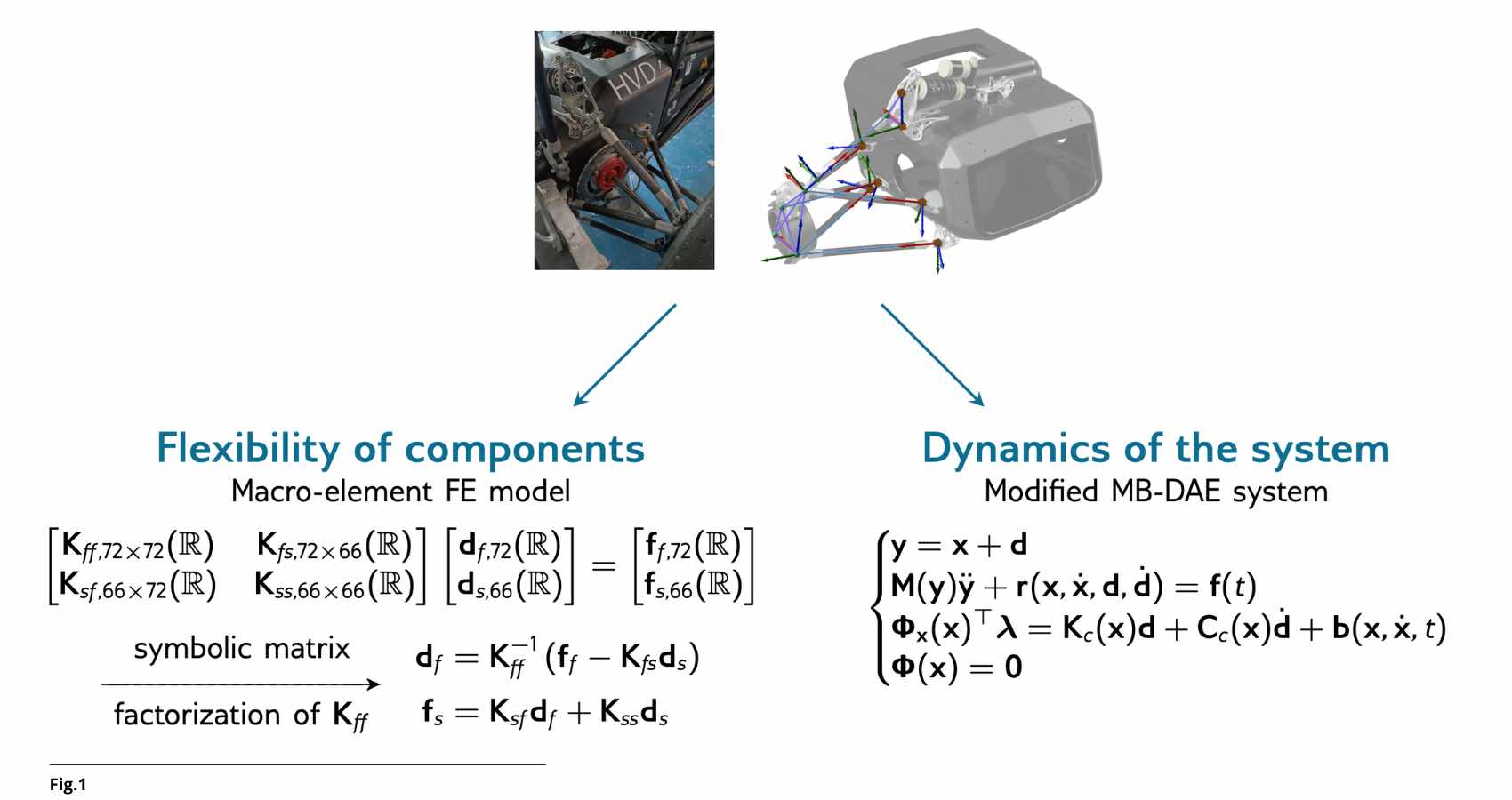
A meaningful case study involves simulating the dynamic behavior of an automotive suspension.
The model includes both differential equations (mass motion) and algebraic equations (spring and rigid-arm constraints), producing a system of index-3 DAEs—among the most challenging to handle.

Elastic deformations of components, modeled as macroscopic finite elements, add further complexity.

The symbolic–numerical approach follows three steps:

1. symbolic formulation of the model using a CAS;
2. reduction and simplification of the DAEs;
3. efficient and stable numerical simulation.
   

The results (Fig.1) show that integrating the two approaches reduces computation time and improves accuracy. In some cases, it even enabled the simulation of systems that would not have been manageable using purely numerical methods.