Calcolo simbolico e numerico insieme per simulare sistemi dinamici complessi

Quando pensiamo a un computer, lo immaginiamo alle prese con numeri: somme, moltiplicazioni, dati che diventano risultati. È il calcolo numerico, quello che usiamo ogni giorno con calcolatrici, fogli di calcolo e software di simulazione.

Ma c’è anche un’altra faccia del calcolo scientifico: il calcolo simbolico. Qui il computer non elabora numeri, ma manipola equazioni e formule, come faremmo noi su carta. I programmi che permettono di farlo si chiamano Computer Algebra Systems (CAS): software capaci di semplificare formule, risolvere sistemi di equazioni e lavorare su modelli matematici complessi.

Il calcolo simbolico, però, ha un limite: quando le equazioni diventano troppo complesse, le formule crescono in modo esponenziale – un fenomeno noto come expression swell. Il calcolo numerico, d’altro canto, è rapido ed efficiente, ma può diventare instabile se il modello è mal condizionato.
La soluzione migliore? Combinare i due mondi.

Il principio è semplice ma potente:

• il calcolo simbolico prepara le equazioni, le semplifica e individua i vincoli del sistema;
• il calcolo numerico esegue poi la simulazione, valutando le equazioni in modo efficiente e preciso.

A seconda del problema, il calcolo simbolico può essere usato solo nella fase iniziale o interagire continuamente con il numerico. Il risultato è sempre lo stesso: simulazioni più robuste, rapide e affidabili.

Un’applicazione: le equazioni differenziali-algebriche (DAE)

Un campo in cui questo approccio dà risultati notevoli è quello delle equazioni differenziali-algebriche (DAE), che combinano due tipi di relazioni:

• differenziali, che descrivono l’evoluzione nel tempo;
• algebriche, che impongono vincoli sul comportamento del sistema.

Le DAE sono fondamentali in ingegneria per descrivere sistemi complessi: veicoli, robot, circuiti elettrici o persino missioni spaziali.
Contengono vincoli intrinseci (come le giunture di un robot o le leggi di Kirchhoff in un circuito) che rendono il modello realistico ma anche difficile da simulare.
Qui il calcolo simbolico mostra tutta la sua utilità: riscrivendo e semplificando le DAE, consente ai metodi numerici di operare con maggiore stabilità e velocità.

Un esempio: la sospensione di un veicolo

Un caso di studio significativo riguarda la simulazione del comportamento dinamico di una sospensione automobilistica.
Il modello comprende sia equazioni differenziali (movimento delle masse) sia equazioni algebriche (vincoli di molle e bracci rigidi), portando a un sistema di DAE di indice 3, tra i più complessi da trattare.
Le deformazioni elastiche delle componenti, modellate come elementi finiti macroscopici, aggiungono ulteriore difficoltà.

L’approccio simbolico-numerico segue tre passaggi:

1. formulazione simbolica del modello con un CAS;
2. riduzione e semplificazione delle DAE;
3. simulazione numerica efficiente e stabile.

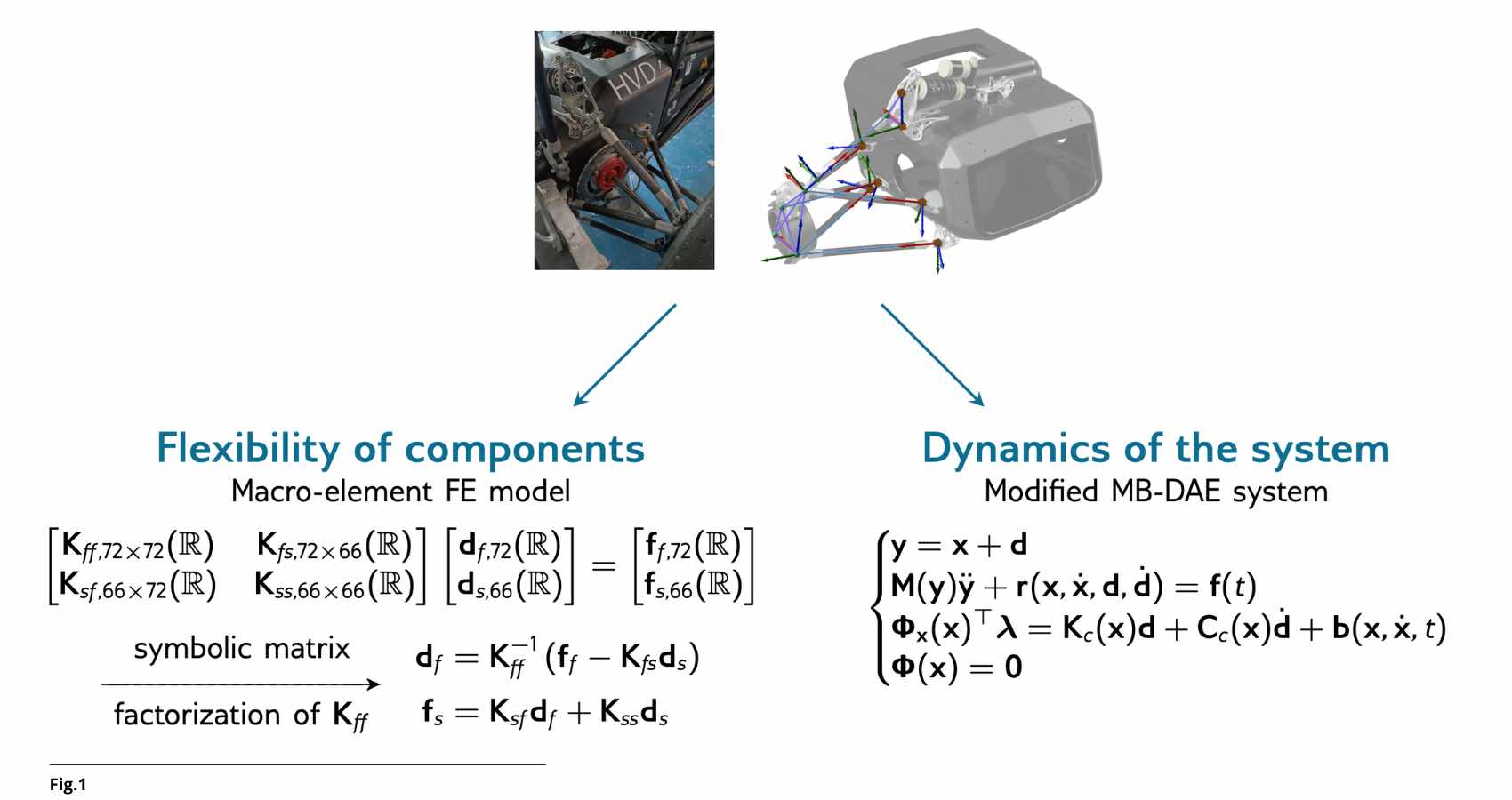
I risultati (Fig.1) mostrano che l’integrazione dei due approcci riduce i tempi di calcolo e migliora la precisione.
In alcuni casi, ha reso possibile simulare sistemi che con metodi puramente numerici non sarebbero stati gestibili.